Notes

Improving your Profile Using Github

• Important sections that represent who you are as a developer:
  • Followers & Following
  • Stars (likes)
  • Green Gardens
  • Photo and Brief Intro

Wikis (Pre-Project)

• Best Practices for Wiki Creation:

  • List of technologies used.
  • Separate design documents into their own sections.
  • Write clearly and concisely, grammar is important!

• MVP : Minimum Viable Product - Outline of your project’s features on your Repo Wiki.

• Example of a MVP :
  • Users are able to log into application
  • Users are able to create, edit, and delete tweets
  • Users are able to follow other users and see their tweets
  • Users are able to like other users tweets
  • Users are able to comment on other users tweets

README FIles (Post-Project)

• Consider README’s as first impressions to prospective employers.
• Readme’s are done in markdown.
• Readme Best Practices:
  • Divide your README into distinct sections
  • List the technologies used at the top of your README for increased visibility
  • Include nice pictures or Gifs to show and/or demonstrate how things work
  • Include code snippets
  • Provide instructions for how to install project (if applicable)
  • Include link to the live site

Github Identity

• Github is a community of developers, and is a place to share, build, and discover software (also VC).

Big O Notation

• Big O helps gives us a precise vocabulary to talk about how our code performs.

  • Useful for discussing trade-offs between different approaches.
  • Helps us debug things easier.
  • It also comes up a lot in interviews!

• An Example: Comparing two functions that calculate the sum of all numbers from 1 up to n.

function addUpTo(n) {
  let total = 0;
  for (let i = 0; i <= n; i++) {
    total += i;
  }
  return total;
}

Number of operations will grow with n. Would be O(n) or Linear Time.

function addUpTo(n) {
  return (n * (n + 1)) / 2;
}

Has three simple operations: 1 Multiplication 1 Addition 1 Division. (Regardless of n) Would be O(1) or Constant Time.

• First we need to consider what makes one implementation better than the other?

  • Faster? (Time Complexity);
  • Less Memory Intensive (Space Complexity);
  • More Readable

• How can we measure speed?

  • Timers? (Doesn’t work well - not reliable or precise)
  • Instead we should count the number of simple operations.
• Big O Notation is a way to formalize fuzzy counting.
• An algorithm is O(f(n)) if the number of simple operations the computer has to do is eventually less than a constant f(n) times, as n increases.
  • f(n) = n (Linear)
  • f(n) = n^2 (Quadratic)
  • f(n) = 1 (Constant)
  • f(n) could be anything!

function countUpAndDown(n) {
  console.log('going up!');
  for (let i = 0; i < n; i++) {
    console.log(i);
  }
  console.log('at the top, going down!');
  for (let j = n - 1; j >=0; j--) {
    console.log(j);
  }
  console.log('Back down, bye!);
}

Both loops are O(n) but since we just want the big picture, this entire function would be O(n);

function printAllPairs(n) {
  for (var i = 0; i < n; i++) {
    for (var j = 0; j < n; j++) {
      console.log(i, j);
    }
  }
}

Nested loops are never a good thing when trying to write fast code. O(n^2) or Quadratic Time.

• Constants don’t matter in big O & Smaller Terms don’t matter

  • O(2n) is just O(n) Linear
  • O(500) is just O(1) Constnat
  • O(13n^2) is just O(n^2) Quadratic
  • O(n + 10) is just O(n) Linear
  • O(1000n + 50) is just O(n) Linear
  • O(n^2 + 5n + 8) is just O(n^2) Quadratic

• Big O Shorthands

  • Arithmetic Operations are Constant
  • Variable assignment is constant
  • Accessing elements in an array (by index) or by object (by key) is constant.
  • In a loop, the complexity is the length of the loop times the complexity of whatever is inside of the loop.

• Additional Examples

function logAtLeast5(n) {
  for (var i = 1; i <= Math.max(5, n); i++) {
    console.log(i);
  }
}

O(n) Linear Time

function logAtMost5(n) {
  for (var i = 1; i <= Math.min(5, n); i++) {
    console.log(i);
  }
}

O(1) Constant Time.

A Guide to Big-O Notation

Curating Complexity: A Guide to Big-O Notation

• Why is looking at runtime not a reliable method of calculating time complexity?

  • Not all computers are made equal( some may be stronger and therefore boost our runtime speed )
  • How many background processes ran concurrently with our program that was being tested?
  • We also need to ask if our code remains performant if we increase the size of the input.

• The real question we need to answering is: How does our performance scale?.

Big O Notation

• Big O Notation is a tool for describing the efficiency of algorithms with respect to the size of the input arguments.
• Since we use mathematical functions in Big-O, there are a few big picture ideas that we’ll want to keep in mind:
  • The function should be defined by the size of the input.
  • Smaller Big O is better (lower time complexity)
  • Big O is used to describe the worst case scenario.
  • Big O is simplified to show only its most dominant mathematical term.

Simplifying Math Terms

• We can use the following rules to simplify the our Big O functions:

  • Simplify Products : If the function is a product of many terms, we drop the terms that don’t depend on n.
  • Simplify Sums : If the function is a sum of many terms, we drop the non-dominant terms.
• n : size of the input
• T(f) : unsimplified math function

• O(f) : simplified math function.

Simplifying a Product | Unsimplified | Big-O Simplified | | ——————- | ——————— | | T(5 _ n^2) | O(n^2) Quadratic | | T(100000 _ n) | O(n) Linear | | T( n / 12) | O (n) Linear | | T( 42 _ n _ log(n)) | O(nlog(n)) Log Linear | | T(12) | O(1) Constant |

Simplifying a Sum | Unsimplified | Big-O Simplified | | —————- | —————— | | T( n3 + n2 + n ) | O(n^3) | | T( log(n) + 2n ) | O(2^n) Exponential | | T( n + log(n) ) | O(n) Linear | | T( n! + 10n ) | O(n!) Polynomial |

Putting it all together

• First we apply the product rule to drop all constants.
• Then we apply the sum rule to select the single most dominant term.

Complexity Classes

Common Complexity Classes

There are 7 major classes in Time Complexity

• O(1) Constant

  • The algorithm takes roughly the same number of steps for any input size.

  // O(1)
  function constant1(n) {
    return n * 2 + 1;
  }
  
  // O(1)
  function constant2(n) {
    for (let i = 1; i <= 100; i++) {
      console.log(i);
    }
  }

• O(log(n)) Logarithmic

  • In most cases our hidden base of Logarithmic time is 2, log complexity algo’s will typically display ‘halving’ the size of the input (like binary search!)

  // O(log(n))
  function logarithmic1(n) {
    if (n <= 1) return;
    logarithmic1(n / 2);
  }
  
  // O(log(n))
  function logarithmic2(n) {
    let i = n;
    while (i > 1) {
      i /= 2;
    }
  }

• O(n) Linear

  • Linear algo’s will access each item of the input “once”.

  // O(n)
  function linear1(n) {
    for (let i = 1; i <= n; i++) {
      console.log(i);
    }
  }
  
  // O(n), where n is the length of the array
  function linear2(array) {
    for (let i = 0; i < array.length; i++) {
      console.log(i);
    }
  }
  
  // O(n)
  function linear3(n) {
    if (n === 1) return;
    linear3(n - 1);
  }

• O(nlog(n)) Log Linear Time
  • Combination of linear and logarithmic behavior, we will see features from both classes.
  • Algo’s that are log-linear will use both recursion AND iteration.

// O(n * log(n))
function loglinear(n) {
  if (n <= 1) return;

  for (let i = 1; i <= n; i++) {
    console.log(i);
  }

  loglinear(n / 2);
  loglinear(n / 2);
}

• O(nc) Polynomial
  • C is a fixed constant.

// O(n^2)
function quadratic(n) {
  for (let i = 1; i <= n; i++) {
    for (let j = 1; j <= n; j++) {}
  }
}

// O(n^3)
function cubic(n) {
  for (let i = 1; i <= n; i++) {
    for (let j = 1; j <= n; j++) {
      for (let k = 1; k <= n; k++) {}
    }
  }
}

• Example of Quadratic and Cubic runtime.

• O(c^n) Exponential
  • C is now the number of recursive calls made in each stack frame.
  • Algo’s with exponential time are VERY SLOW.

// O(2^n)
function exponential2n(n) {
  if (n === 1) return;
  exponential_2n(n - 1);
  exponential_2n(n - 1);
}

// O(3^n)
function exponential3n(n) {
  if (n === 0) return;
  exponential_3n(n - 1);
  exponential_3n(n - 1);
  exponential_3n(n - 1);
}

• O(n!) Factorial
  • The largest/ worst complexity (minus DTIME which is n^n);

Memoization

• Memoization : a design pattern used to reduce the overall number of calculations that can occur in algorithms that use recursive strategies to solve.
  • MZ stores the results of the sub-problems in some other data structure, so that we can avoid duplicate calculations and only ‘solve’ each problem once.
  • Two features that comprise memoization:
    • 1. FUNCTION MUST BE RECURSIVE.
    • 2. Our additional DS is usually an object (we refer to it as our memo!)

Memoizing Factorial

let memo = {};

function factorial(n) {
  // if this function has calculated factorial(n) previously,
  // fetch the stored result in memo
  if (n in memo) return memo[n];
  if (n === 1) return 1;

  // otherwise, it havs not calculated factorial(n) previously,
  // so calculate it now, but store the result in case it is
  // needed again in the future
  memo[n] = n * factorial(n - 1);
  return memo[n];
}

factorial(6); // => 720, requires 6 calls
factorial(6); // => 720, requires 1 call
factorial(5); // => 120, requires 1 call
factorial(7); // => 5040, requires 2 calls

memo; // => { '2': 2, '3': 6, '4': 24, '5': 120, '6': 720, '7': 5040 }

• Our memo object is mapping out our arguments of factorial to it’s return value.
  • Keep in mind we didn’t improve the speed of our algo.

Memoizing Fibonacci

• Our time complexity for fibonacci goes from O(2^n) to O(n) after applying memoization.

The Memoization Formula

Rules

1. Write the unoptimized brute force recursion (make sure it works);
2. Add memo object as an additional arugmnt .
3. Add a base case condition that returns the stored value if the function’s argument is in the memo.
4. Before returning the result of the recursive case, store it in the memo as a value and make the function’s argument it’s key.

Things to remember

1. When solving DP problems with Memoization, it is helpful to draw out the visual tree first.
2. When you notice duplicate sub-tree’s that means we can memoize.

**

function fastFib(n, memo = {}) {
  if (n in memo) return memo[n];
  if (n === 1 || n === 2) return 1;

  memo[n] = fastFib(n - 1, memo) + fastFib(n - 2, memo);
  return memo[n];
}

fastFib(6); // => 8
fastFib(50); // => 12586269025

Tabulation

• Tabulation Strategy
  • Use When:
    • The function is iterative and not recursive.
    • The accompanying DS is usually an array.

function fib(n) {
  let mostRecentCalcs = [0, 1];

  if (n === 0) return mostRecentCalcs[0];

  for (let i = 2; i <= n; i++) {
    const [secondLast, last] = mostRecentCalcs;
    mostRecentCalcs = [last, secondLast + last];
  }

  return mostRecentCalcs[1];
}

• Steps for tabulation
  • Create a table array based off the size of the input.
  • Initialize some values in the table to ‘answer’ the trivially small subproblem.
  • Iterate through the array and fill in the remaining entries.
  • Your final answer is usually the last entry in the table.

Class Examples

Example of Linear Search

function search(array, term) {
  for (let i = 0; i < array.length; i++) {
    if (array[i] === term) {
      return i;
    }
  }
  return -1;
}

• Worst Case Scenario: The term does not even exist in the array.
• Meaning: If it doesn’t exist then our for loop would run until the end therefore making our time complexity O(n).

Example of Binary Search

function binarySearch(arr, x, start, end) {
  if (start > end) return false;

  let mid = Math.floor((start + end) / 2);
  if (arr[mid] === x) return true;

  if (arr[mid] > x) {
    return binarySearch(arr, x, start, mid - 1);
  } else {
    return binarySearch(arr, x, mid + 1, end);
  }
}

• Must be conducted on a sorted array.
• Binary search is logarithmic time, not exponential b/c n is cut down by two, not growing.
• Binary Search is part of Divide and Conquer.

Example of Merge Sort

function merge(leftArray, rightArray) {
  const sorted = [];
  while (letArray.length > 0 && rightArray.length > 0) {
    const leftItem = leftArray[0];
    const rightItem = rightArray[0];

    if (leftItem > rightItem) {
      sorted.push(rightItem);
      rightArray.shift();
    } else {
      sorted.push(leftItem);
      leftArray.shift();
    }
  }

  while (leftArray.length !== 0) {
    const value = leftArray.shift();
    sorted.push(value);
  }

  while (rightArray.length !== 0) {
    const value = rightArray.shift();
    sorted.push(value);
  }

  return sorted;
}

function mergeSort(array) {
  const length = array.length;
  if (length === 1) {
    return array;
  }

  const middleIndex = Math.ceil(length / 2);
  const leftArray = array.slice(0, middleIndex);
  const rightArray = array.slice(middleIndex, length);

  leftArray = mergeSort(leftArray);
  rightArray = mergeSort(rightArray);

  return merge(leftArray, rightArray);
}

Example of Bubble Sort

function bubbleSort(items) {
  var length = items.length;
  for (var i = 0; i < length; i++) {
    for (var j = 0; j < length - i - 1; j++) {
      if (items[j] > items[j + 1]) {
        var tmp = items[j];
        items[j] = items[j + 1];
        items[j + 1] = tmp;
      }
    }
  }
}

• Worst Case & Best Case are always the same because it makes nested loops.
• Double for loops are polynomial time complexity or more specifically in this case Quadratic big O O(n^2); # Notes

Sorting Algorithms

Bubble Sort

• The first major sorting algorithm one learns in introductory programming courses.
• Gives an intro on how to convert unsorted data into sorted data.
• It’s almost never used in production code because:
  • It’s not efficient
  • It’s not commonly used
  • There is stigma attached to it

• Bubbling Up : Term that infers that an item is in motion, moving in some direction, and has some final resting destination.

• Bubble sort, sorts an array of integers by bubbling the largest integer to the top.

// Bubble Sort
function bubble(array) {
  let sorted = true;
  for (let i = 0; i < array.length; i++) {
    let num1 = array[i];
    let num2 = array[i + 1];
    if (num1 > num2) {
      array[i + 1] = num1;
      array[i] = num2;
      sorted = false;
    }
  }
  if (sorted) {
    return array;
  } else {
    return bubble(array);
  }
}

Selection Sort

• Selection sort organizes the smallest elements to the start of the array.
• Summary of how Selection Sort should work:
  1. Set MIN to location 0
  2. Search the minimum element in the list.
  3. Swap with value at location Min
  4. Increment Min to point to next element.
  5. Repeat until list is sorted.

let selectionSort = (arr) => {
  let len = arr.length;
  for (let i = 0; i < len; i++) {
    let min = i;
    for (let j = i + 1; j < len; j++) {
      if (arr[min] > arr[j]) {
        min = j;
      }
    }
    if (min !== i) {
      let tmp = arr[i];
      arr[i] = arr[min];
      arr[min] = tmp;
    }
  }
  return arr;
};

Selection Sort

Time Complexity: Quadratic O(n^2)

• Our outer loop will contribute O(n) while the inner loop will contribute O(n / 2) on average. Because our loops are nested we will get O(n^2);

Space Complexity: O(1)

• Selection Sort will always use the same amount of memory regardless of n.

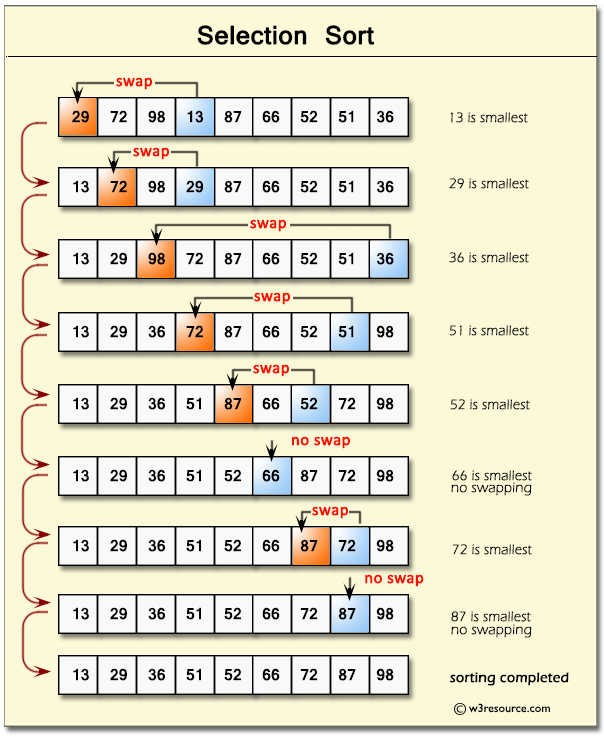
Class Solution

function swap(array, idx1, idx2) {
  [array[idx1], array[idx2]] = [array[idx2], array[idx2]];
}

function selectionSort(array) {
  for (let i = 0; i < array.length; i++) {
    let lowest = i;
    for (let j = i + 1; j < array.length; j++) {
      if (list[j] < list[lowest]) {
        lowest = j;
      }
    }
    if (place !== i) {
      swap(array, i, lowest);
    }
  }
}

Alt Solution

function selectionSort(array) {
  for (let i = 0; i < array.length; i++) {
    let lowest = i;
    for (let j = 0; j < array.length; j++) {
      if (array[j] < array[i]) {
        lowest = j;
      }
    }
    if (lowest !== i) {
      let temp = array[i];
      array[i] = array[lowest];
      array[lowest] = temp;
    }
  }
  return array;
}

Insertion Sort

Time Complexity: Quadratic O(n^2)

• Our outer loop will contribute O(n) while the inner loop will contribute O(n / 2) on average. Because our loops are nested we will get O(n^2);

Space Complexity: O(n)

• Because we are creating a subArray for each element in the original input, our Space Comlexity becomes linear.

Class Solution

function insertionSort(array) {
  for (let i = 1; i < array.length; i++) {
    let value = list[i];
    let hole = i;
    while (hole > 0 && list[hole - 1] > value) {
      list[hole] = list[hole - 1];
      hole--;
    }
    list[hole] = value;
  }
  return array;
}

Alt Solution

function insertionSort(arr) {
  for (let i = 1; i < arr.length; i++) {
    let current = arr[i];
    let j = i - 1;
    while (j > -1 && current < arr[j]) {
      arr[j + 1] = arr[j];
      j--;
    }
    arr[j + 1] = current;
  }
  return arr;
}

Merge Sort

Time Complexity: Log Linear O(nlog(n))

• Since our array gets split in half every single time we contribute O(log(n)). The while loop contained in our helper merge function contributes O(n) therefore our time complexity is O(nlog(n)); Space Complexity: O(n)
• We are linear O(n) time because we are creating subArrays.

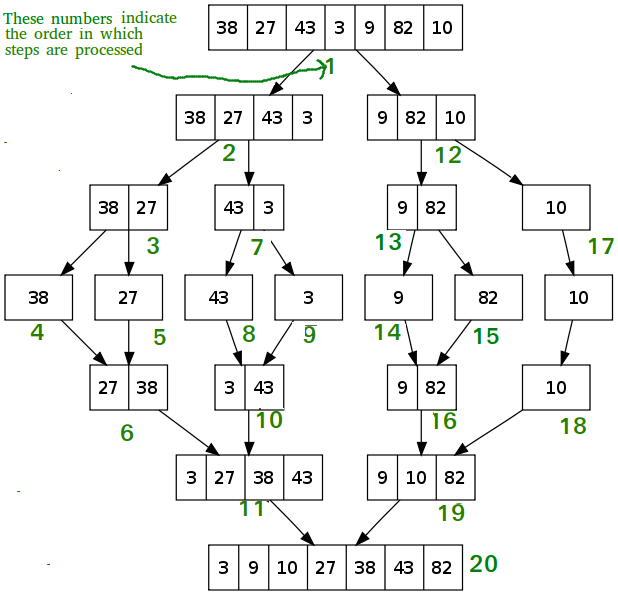
Class Solution

function merge(arr1, arr2) {
  let result = [];
  while (arr1.length && arr2.length) {
    if (arr1[0] < arr2[0]) {
      result.push(arr1.shift());
    } else {
      result.push(arr2.shift());
    }
  }
  return [...result, ...arr1, ...arr2];
}

function mergeSort(arr) {
  if (arr.length <= 1) return arr;

  const mid = Math.floor(arr.length / 2);
  const left = mergeSort(arr.slice(0, mid));
  const right = mergeSort(arr.slice(mid));

  return merge(left, right);
}

Quick Sort

Time Complexity: Quadratic O(n^2)

• Even though the average time complexity O(nLog(n)), the worst case scenario is always quadratic.

Space Complexity: O(n)

• Our space complexity is linear O(n) because of the partition arrays we create.

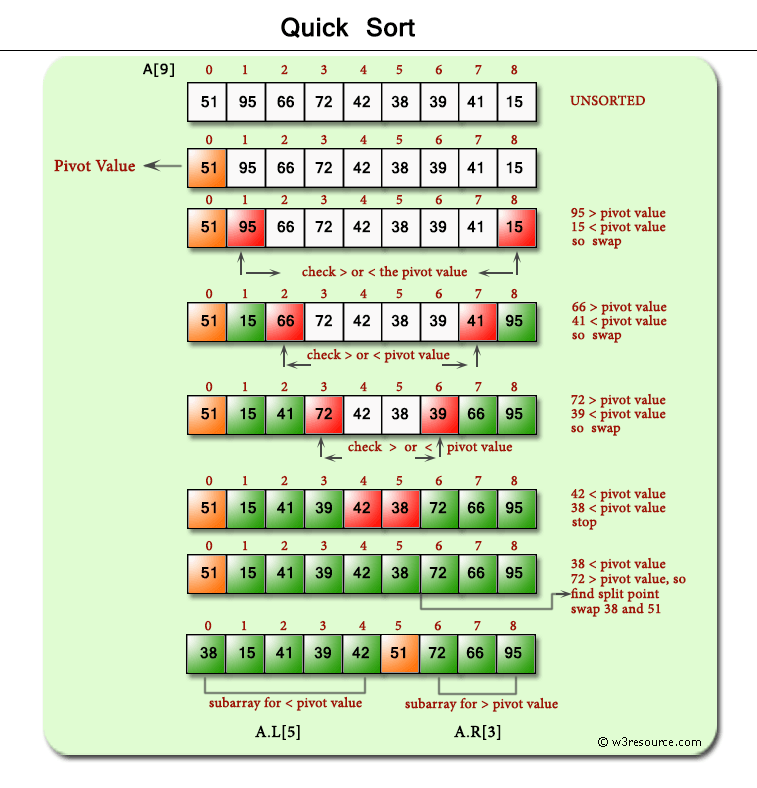
function quickSort(array) {
  if (array.length <= 1) return array;

  let pivot = array.shift();

  let left = array.filter((x) => x < pivot);
  let right = array.filter((x) => x >= pivot);

  let sortedLeft = quickSort(left);
  let sortedRight = quickSort(right);

  return [...sortedLeft, pivot, ...sortedRight];
}

Binary Search

Time Complexity: Log Time O(log(n))

Space Complexity: O(1)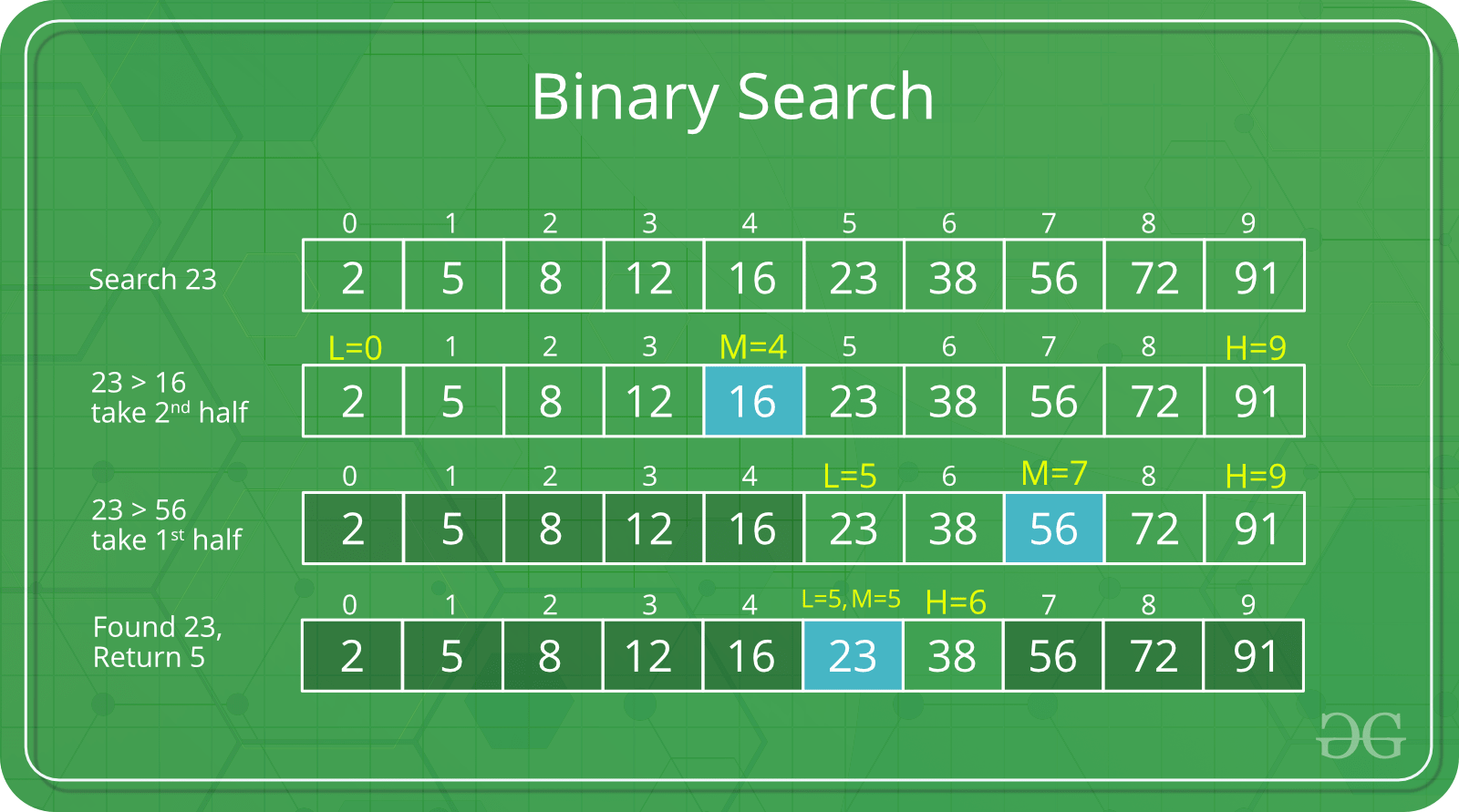

Recursive Solution

function binarySearch(array, target) {
  if (array.length === 0) return false;

  let midPt = Math.floor(array.length / 2);

  if (array[midPt] === target) {
    return true;
  } else if (list[midPt] > target) {
    return binarySearch(list.slice(0, mid), target);
  } else {
    return binarySearch(list.slice(midPt + 1), target);
  }
}

Min Max Solution

function binarySearch(array, target) {
  let start = 0;
  let end = array.length - 1;

  while (start <= end) {
    let midpoint = Math.floor((start + end) / 2);

    if (target === array[midpoint]) {
      return midpoint;
    }

    if (target > array[midpoint]) {
      start = midpoint + 1;
    }

    if (target < array[midpoint]) {
      end = midpoint - 1;
    }
  }
  return -1;
}

Insertion Sort

• Works by building a larger and larger sorted region at the left-most end of the array.
• Steps:
  1. If it is the first element, and it is already sorted; return 1.
  2. Pick next element.
  3. Compare with all elements in the sorted sub list
  4. Shift all the elemnts in the sorted sub list that is greater than the value to be sorted.
  5. Insert the value
  6. Repeat until list is sorted.

let insertionSort = (inputArr) => {
  let length = inputArr.length;
  for (let i = 1; i < length; i++) {
    let key = inputArr[i];
    let j = i - 1;
    while (j >= 0 && inputArr[j] > key) {
      inputArr[j + 1] = inputArr[j];
      j = j - 1;
    }
    inputArr[j + 1] = key;
  }
  return inputArr;
};

Merge Sort

• Merge sort is nlogn time.
• We need a function for merging and a function for sorting.
• Steps:
  1. If there is only one element in the list, it is already sorted; return the array.
  2. Otherwise, divide the list recursively into two halves until it can no longer be divided.
  3. Merge the smallest lists into new list in a sorted order.

const merge = (arr1, arr2) => {
  let sorted = [];

  while (arr1.length && arr2.length) {
    if (arr1[0] < arr2[0]) sorted.push(arr1.shift());
    else sorted.push(arr2.shift());
  }

  return sorted.concat(arr1.slice().concat(arr2.slice()));
};

const mergeSort = (arr) => {
  if (arr.length <= 1) return arr;
  let mid = Math.floor(arr.length / 2),
    left = mergeSort(arr.slice(0, mid)),
    right = mergeSort(arr.slice(mid));

  return merge(left, right);
};

Quick Sort

• QS is another Divide and Conquer strategy.
• Some key ideas to keep in mind:
  • It is easy to sort elements of an array relative to a particular target value.
  • An array of 0 or 1 elements is already trivially sorted.

function quick_Sort(origArray) {
  if (origArray.length <= 1) {
    return origArray;
  } else {
    var left = [];
    var right = [];
    var newArray = [];
    var pivot = origArray.pop();
    var length = origArray.length;

    for (var i = 0; i < length; i++) {
      if (origArray[i] <= pivot) {
        left.push(origArray[i]);
      } else {
        right.push(origArray[i]);
      }
    }

    return newArray.concat(quick_Sort(left), pivot, quick_Sort(right));
  }
}

binary search

const binarySearch = (array, target) => {
  let startIndex = 0;
  let endIndex = array.length - 1;
  while(startIndex <= endIndex) {
    let middleIndex = Math.floor((startIndex + endIndex) / 2);
    if(target === array[middleIndex) {
      return console.log("Target was found at index " + middleIndex);
    }
    if(target > array[middleIndex]) {
      console.log("Searching the right side of Array")
      startIndex = middleIndex + 1;
    }
    if(target < array[middleIndex]) {
      console.log("Searching the left side of array")
      endIndex = middleIndex - 1;
    }
    else {
      console.log("Not Found this loop iteration. Looping another iteration.")
    }
  }

  console.log("Target value not found in array");
}

Notes

Linked Lists

• A linked list represents a linear sequence of ‘vertices’ or ‘nodes’ and tracks three properties.
  • Head : The first node in the list.
  • Tail : The last node in the list.
  • Length : The number of nodes in the list; the list’s length.
• Nodes : Simpler, smaller data structure that connects the linked list.
• Node Properties:
  • Value : THe actual value this node represents.
  • Next : The next node in the list (relative to this node).
  • Previous : The previous node in the list (relative to this node).